Stochastic and Diffusive Processes W23/24
to Whiteboard Site
Content
Stochastic processes are mathematical models used to describe the dynamics of random phenomena
and are widely applied in many disciplines ranging from physics, chemistry, biology, and economics.
During the course, students will learn both the theory underlying stochastic processes and advanced numerical
methods to solve problems with real applications.
Github repository which collects the jupyter notebooks and the notes presented in class. The notebooks can be opened and used in the browser by means of binder (no need to download/install anything).
Lecture 13: Conclusion and overview of the course
Lecture 12: Fuzzy clustering and PCCA+
Suggested readings
Lecture 11: Square Root Approximation (SqRA) of the infinitesimal generator
Suggested readings
Lecture 10: Transfer operator formalism
Suggested readings
Lecture 9: Kramers rate theory for low friction regime
- Lecture notes 9 (Work in progress...)
- Lecture 9, jupyter notebooks
Suggested readings
Lecture 8: Kramers rate theory for moderate and high friction regime
- Lecture notes 8 (Work in progress...)
- Lecture 8, jupyter notebooks
- Exercise 8
Suggested readings
Lecture 7: Introduction to escape rate problem, backward Kolmogorov equation, Mean First Passage Time, Pontryagin's formula, Ornstein_Uhlenbeck process, integration schemes for SDEs
Suggested readings
Lecture 6: Fluctuation-Dissipation Theorem; overview of Fourier analysis; from Generalized Langevin Equation to Langevin Dynamics; introduction to Stochastic Calculus; System Size expansion method for Master equations
Suggested readings
Lecture 5: Overview of Hamiltonian dynamics and Statistical Mechanics; The Generalized Langevin Equation: the memory kernel and the noise term
- Lecture notes 5
- Notes Hamiltonian Dynamics
- Notes Statistical Mechanics
- Notes integrators
- Lecture 5, jupyter notebooks
Suggested readings
Lecture 4: Derivation of the Generalized Langevin Equation from the Kac-Zwanzig model (4a); method of generating function and Gillespie's algorithm to solve the master equation (4b)
- Lecture notes 4a
- Lecture notes 4b
- Lecture 4, jupyter notebooks
- Exercise 4
- Exercise 4, jupyter notebooks
Suggested readings
- Tuckerman M.E., Statistical Mechanincs: Theory and Molecular Simulation 2010, Chapter 15
- Gillespie D.T., Markov Processes 1992, Chapter 5
- Shorack G.R., Probability for statisticians 2000, Chapter 7
Lecture 3: Markov processes, derivation of Chapman-Kolmogorv equation, Kramers-Moyal expansion, master equation, Fokker-Planck equation, Pawula theorem
Suggested readings
Lecture 2: Overview of probability theory and statistics
Suggested readings
Lecture 1: Brownian motion, Einstein's theory, Langevin's theory
Suggested readings
- Gardiner W., Handbook of Stochastic Methods 1994, chapter 1
- Brown R. 1828
- Einstein A. 1905
- Langevin P. 1908
- Simulation of Brownian motion (video)
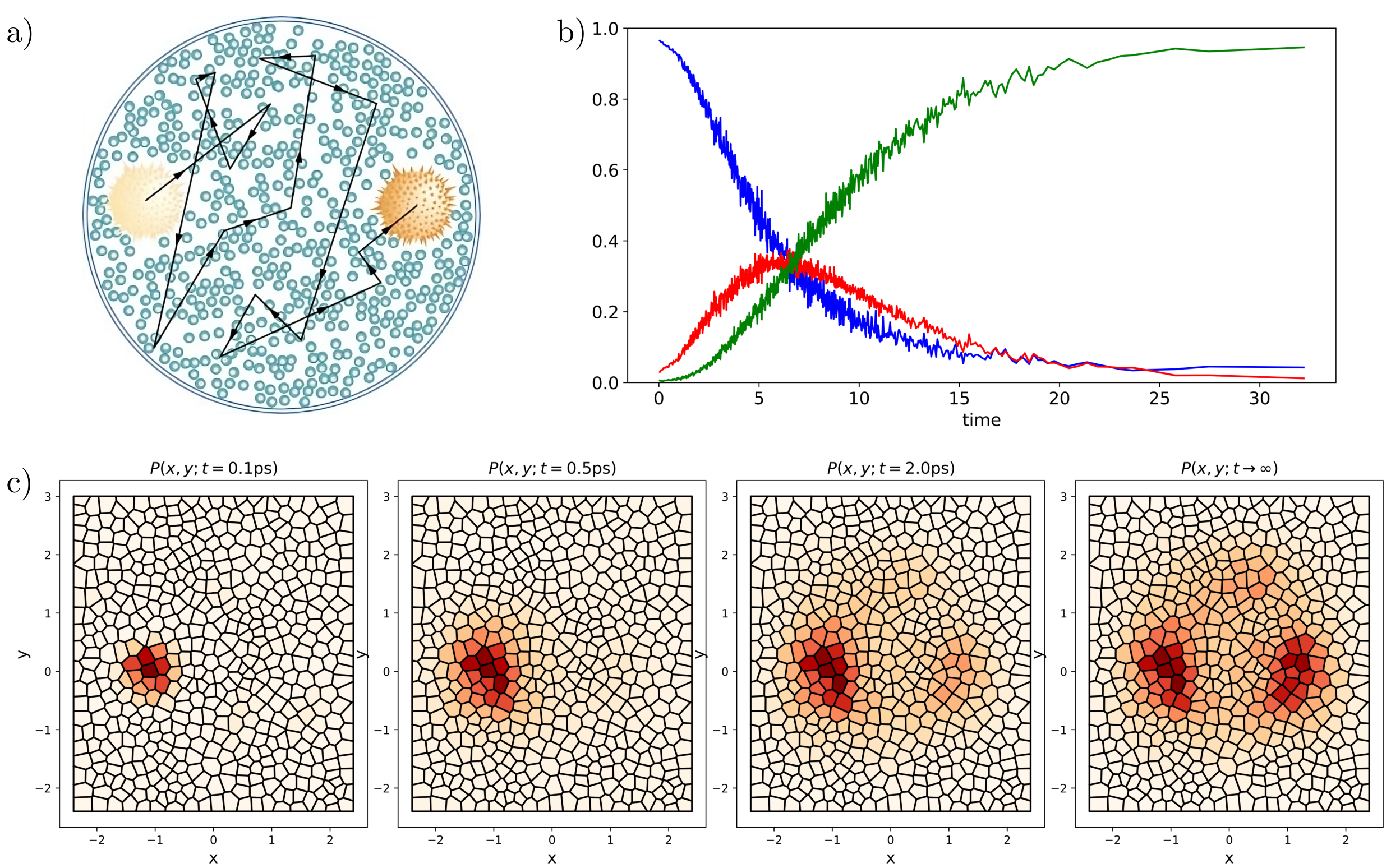
Figure. (a) Brownian motion; (b) Solution of the SIR model generated by Gillespie algorithm; (c) Solution of the Fokker-Planck equation generated by SqRA.
| Course No | Course Type | Hours |
|---|---|---|
| 19242101 | Vorlesung | 2 |
| 19242102 | Übung | 2 |
| Time Span | 17.10.2023 - 13.02.2024 |
|---|---|
| Instructors |
Luca Donati
|
| 0089c_MA120 | 2014, MSc Informatik (Mono), 120 LPs |
| 0280b_MA120 | 2011, MSc Mathematik (Mono), 120 LPs |
| 0280c_MA120 | 2018, MSc Mathematik (Mono), 120 LP |
Stochastic and Diffusive Processes W23/24
to Whiteboard Site
| Day | Time | Location | Details |
|---|---|---|---|
| Tuesday | 14-16 | A6/SR 009 Seminarraum | 2023-10-17 - 2024-02-13 |
| Day | Time | Location | Details |
|---|---|---|---|
| Tuesday | 12-14 | T9/046 Seminarraum | Übung 01 |
Stochastic and Diffusive Processes W23/24
to Whiteboard Site
2023-10-18: Welcome!
Dear Students,
Welcome to the course 'Stochastik IV: Stochastic and Diffusive Processes'.
Tomorrow there will be the introduction to the course, then the first lesson on Brownian Motion, Einstein, and Langevin theory.
See you at 12 pm in T9/SR046!
Best,
Luca Donati
Published by: Luca Donati
Stochastic and Diffusive Processes W23/24
to Whiteboard Site
Or at least none which you're allowed to see with your current set of permissions.
Maybe you have to log in first.